At thermal equilibrium, the transverse magnetisation component (Mxy) is zero and the longitudinal magnetisation component Mz is denoted as M0. For simplicity, M0 is often set to 1 in signal simulations. This makes it more straightforward to assess the values of Mxy and Mz relative to M0, which is their maximum possible value. The relaxation rate of Mz depends on its value relative to M0.
The Bloch equation (Eq. 1) provides a classical description of the magnetisation evolution over time.
The second term (Eq. 2) describes how Mz relaxes back to its thermal equilibrium orientation (M0) after a perturbation.
The solution to this term (Eq. 3) shows how Mz(t) depends on the equilibrium magnetisation M0, the starting magnetisation Mz(0), the time delay t and the time constant T1.
Longitudinal relaxation is sometimes quoted in terms of relaxation rate R1, which is 1/T1. The time constant T1 depends on spin-lattice interactions, where energy is transferred between the spins and the neighbouring lattice of molecules. This energy exchange depends on the movement of the molecules in the lattice, making it temperature-dependent. It increases with the static magnetic field strength and is affected by the types of molecules in the lattice, including the concentration of unbound water.
Methods to measure T1 must isolate the effect of T1 on the acquired MR signal. Conventional strategies often use spin-echo sequences with an initial inversion preparation pulse to induce T1 sensitivity. To map T1, fully relaxed initial magnetisation is assumed and an inversion pulse is applied to invert the sign of Mz. This is followed by an excitation pulse to rotate the magnetisation into the transverse plane before an image is acquired, using the shortest possible TE. The delay between the inversion and excitation pulse is known as the Inversion Time (TI). For a constant TE, the magnetisation component at the time of the excitation pulse varies with TI, as shown in Eq. 4. The Inversion recovery model in Eq. 4 is a specific case of Eq. 3.
Equation 4 can be used to calculate that after TI = 5T1 the longitudinal magnetisation Mz has returned to 98.7% of M0 and can therefore be regarded as fully relaxed.
Figure 1 demonstrates examples of Mz recovery after an initial inversion, as simulated numerically. Note that Mz recovers after the inversion and crosses zero, before eventually plateauing at M0.
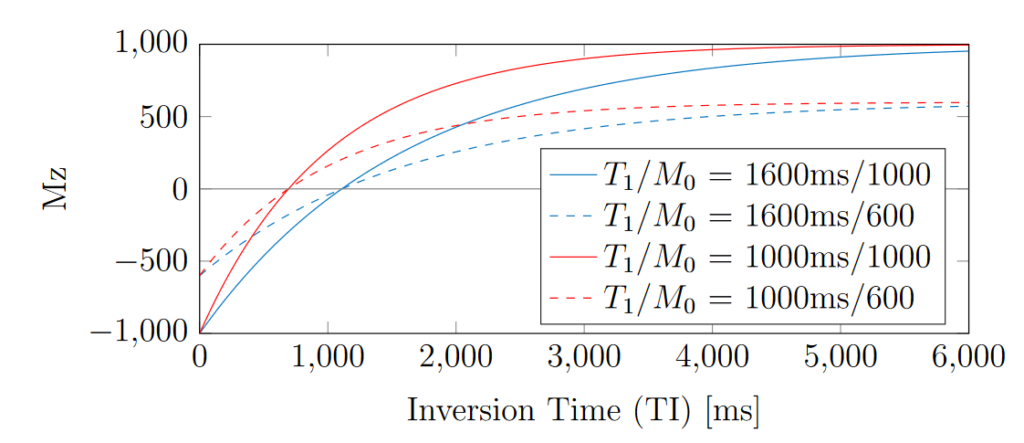
Figure 1. Examples of T1 inversion recovery curves for different T1 and proton density combinations.
The TI at which Mz(TI) = 0 is often called the “null time” and denoted as TInull. This zero-crossing point is important for estimating T1 accurately, as TInull is proportional to T1 and independent from M0. The relationship between TInull and T1 can be derived from Eq. 4 for the case of Mz = 0, as shown in Eq. 5.
In gold standard experiments, the time constant T1 is determined by measuring points on the recovery curves in Fig. 1 and fitting a model based on Eq. 4. Mapping T1 in this way often requires scan times that are too long to be suitable for clinical applications. However, it provides a good reference map for validating new sequences using phantom acquisitions, where more scan time is available. There has been work to design parameter-mapping sequences with reduced scan durations, these include Look-Locker [Crawley1988] and DESPOT1 [Homer1985] for T1. These examples do not require the magnetisation to fully recover between measurements, with DESPOT1 able to provide a 3D T1 map in a clinically feasible scan time [Deoni2003, Nayak2000]. The DESPOT1 sequence uses driven equilibrium signal from a SPoiled Gradient Recalled (SPGR) sequence.
References and Further Reading:
- Allen J. An Optimisation Framework for Magnetic Resonance Fingerprinting. Thesis. 2019.
- A. P. Crawley and R. M. Henkelman. A comparison of oneshot and recovery methods in T1 imaging. Magnetic Resonance in Medicine, 7(1):23–34, 1988
- J. Homer and M. S. Beevers. Driven-equilibrium single-pulse observation of T1 relaxation. A re-evaluation of a rapid ”new” method for determining NMR spin-lattice relaxation times. Journal of Magnetic Resonance, 63(2):287–297, 1985.
- S. C. L. Deoni, B. K. Rutt, and T. M. Peters. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magnetic Resonance in Medicine, 49(3):515–526, 2003.
- K. S. Nayak and D. G. Nishimura. Automatic Field Map Generation and Off-Resonance Correction for Projection Reconstruction Imaging. Magnetic Resonance in Medicine, 43(1):151–154, 2000.
