T2 Introduction

Jack Allen,

Post modified on:

This post considers T2, the time constant that defines the relaxation rate of transverse magnetisation.

From the Bloch equation to the T2 decay curve

As mentioned in the T1 Introduction, at thermal equilibrium the transverse magnetisation component Mxy is zero. The value of Mxy is often assessed relative to M0, its maximum possible value.

To consider Mxy relaxation we must revisit the Bloch equation (Eq. 1).

\begin{equation} \frac{d\mathbf {M}}{dt} = γ\mathbf {M} × \mathbf {B} + \frac{1}{T_1}\left(M_0 − M_z\right) -\frac{M_{xy}}{T_2} \quad [1] \end{equation}

The 3rd term (Eq. 2) describes the decay of Mxy over time.

\begin{equation} \frac{dM_{xy}}{dt} = -\frac{M_{xy}}{T_2} \quad [2] \end{equation}

The solution to Eq. 2 is given in Eq. 3, where Mxy(t) depends on the initial transverse magnetisation Mxy(0), a time delay t and the time constant T2 which represents the rate of transverse magnetisation decay.

\begin{equation} M_{xy}(t) =M_{xy}(0)\exp\left(\frac{-t}{T_2}\right) \quad [3] \end{equation}

The physical basis of T2 relaxation

This decay is caused by dipole interactions between the isochromat population and neighbouring spins of other nuclei and electrons, which lead to fluctuations in the local magnetic field. This spin-spin interaction causes the individual magnetisation vectors of the isochromats to become out of phase, shortening the transverse component in a process known as dephasing.

Dipole interactions depend on the distance between the spins and their relative orientation in terms of the direction of the main magnetic field of the scanner. Free water is able to tumble freely and rapidly and so experiences weak dipole coupling, leading to a relatively long T2. Spins in biological structures are more restricted and so experience faster dephasing, leading to a shortened T2. MRI often makes use of spins in the intracellular or extracellular space, which have a T2 long enough for the signal to be recorded during an imaging experiment and provide information about the tissue structure and function.

T2 and T2*

In practice, additional dephasing occurs due to local field distortions from sources such as system imperfections, subject geometry and tissue boundaries. This means Mxy decays according to T2* (Eq. 4), where T2′ is the decay constant due to reversible dephasing. The presence of T2′ in the expression means T2* is shorter than T2.

\begin{equation} \frac{1}{T_{2}^*} = \frac{1}{T_{2}} + \frac{1}{T_{2}^\prime} \quad [4] \end{equation}

Spin-echoes

Dephasing caused by B0 inhomogeneities can be reversed by playing a 180-degree refocusing pulse after the initial excitation, which flips the magnetisation about one of the transverse axes, inverting the phase distribution of the spins. Assuming the local field inhomogeneities are unchanged the spins will then begin to move back in phase and produce a signal peak (known as a spin-echo) when they are exactly in phase. The elapsed time between the excitation pulse and the occurrence of an echo is known as the Echo Time (TE). For spin-echo sequences TE is twice the time between the excitation pulse and the refocusing pulse. Spin-echo refocusing reverses the decay governed by T2* but the refocused signal peak amplitude still depends on the T2 of the imaged object. Spin-echo sequences are therefore used to produce signal weighted in terms of T2, rather T2* [Allen2019].

Spin-echo sequences form the basis of gold standard T2 mapping. The signal intensity is measured for various TE, which is equivalent to sampling points on the Mxy decay curve of Eq. 3. For gold standard spin-echo T2 mapping, the time between each measurement (i.e. the Repetition Time TR) must be very long compared to T1 (i.e. TR >= 5T1) to ensure full recovery between measurements. The detected signal curves are shown in Fig. 1 [Allen2019] for various combinations of T2 and M0, where it is clear that M0 determines the starting value of Mxy. The curves in Fig. 1 were calculated using Eq. 5.

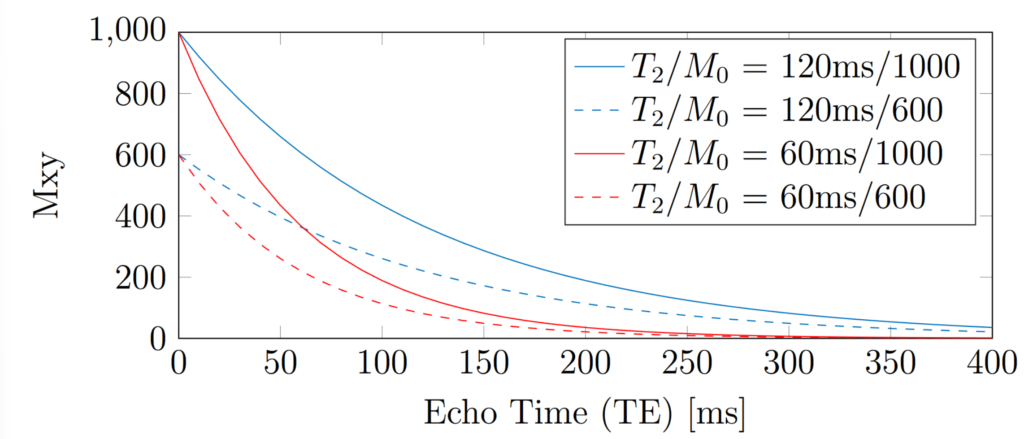
\begin{equation} M_{xy} =M_0 \exp\left(\frac{-TE}{T_2}\right) \quad [5] \end{equation}

Figure 1: Examples of T2 exponential decay curves for different T2 and proton density combinations.

For real gold standard scan data, an image would be acquired for each TE. Across the images, each pixel would possess a signal curve. A signal model (based on Eq. 5) would be fitted to the acquired signal curve of each pixel across the images, allowing T2 to be estimated as a fitted parameter.

Signal offset

To account for positive signal offsets, an additional term C may be included in the fitted model. This is shown in Eq. 6, where STE is the acquired signal.

\begin{equation} S_{TE} =M_0 \exp\left(\frac{-TE}{T_2}\right) + C \quad [6] \end{equation}

For magnitude data with a very low Signal-to-Noise Ratio (SNR) (i.e. below approximately SNR = 3), there is a positive contribution to this offset from the rectification of noise during the imaging acquisition and reconstruction [Allen2019, Gudbjartsson1995]. This means the transverse relaxation curve “plateaus” when TE is long compared to T2. Including an offset term allows better fitting of the data for these cases but introduces some bias for measurements with higher SNR (e.g. shorter TE), potentially introducing error in the fitted T2. Other methods to account for noise rectification include removing the plateaued points from the fit, as demonstrated for T2* in [He2008], or squaring the signal [Miller1993].

The work of Milford et al. demonstrated that imperfect refocusing pulses can contribute to the signal offset in multi-echo spin-echo sequences [Milford2015]. Although the work of [Milford2015] considered a T2-mapping method with multiple echoes measured after each excitation pulse a similar effect could conceivably occur for a single-echo method.

Furthermore, T2 decay can consist of multiple components, leading to multi-exponential decay. There is an offset contribution from long T2 components [Milford2015].

Reducing scan duration

As with T1 mapping, conventional T2 mapping scan durations are unfeasibly long for clinical applications but can provide informative reference maps for testing new sequences and characterising phantoms since more scan time is available for phantom imaging.

Developments to reduce scan durations for T2 mapping include DESPOT2 [Deoni2003, Deoni2005], which requires T1 maps from another acquisition, such as DESPOT1 [Homer1985]. DESPOT2 does not require fully-recovered magnetisation between measurements, allowing a 3D T2 map to be acquired in a clinically feasible scan time. DESPOT2 is based on a Steady State Free Precession (SSFP) sequence. Although DESPOT1 and DESPOT2 offer increased efficiency, it should be noted that both are sensitive to deviations from the prescribed flip angle, which are mainly caused by B1+ inhomogeneity [Deoni2005].

To increase time efficiency, multiple refocusing pulses can be played after each excitation pulse to create a multi-echo spin-echo pulse sequence. Unfortunately, imperfect refocusing reduces the accuracy of T2 mapping this way.

Imperfect refocusing

The Carr-Purcell-Meiboom-Gill (CPMG) conditions [Meiboom1958] reduce the effects of imperfect refocusing pulses by controlling the timing and phase of the refocusing pulses. CPMG sequences create refocused echoes at the mid-point between consecutive refocusing pulses, with consistent phase across the echoes.

Here are the CPMG conditions:

– The refocusing Radio Frequency (RF) pulses are 90 degrees out of phase relative to the excitation pulse.

– The refocusing pulses are equally spaced, where the spacing is twice the interval between the excitation pulse and the first refocusing pulse.

– There is an equal phase accumulation by a spin isochromat between any two consecutive refocusing pulses.

Even under these conditions, there is a residual sensitivity to imperfect refocusing and therefore T2-mapping inaccuracy, particularly for multi-slice imaging [MRIquestions.com, Pell2006].

Turbo Spin-Echo (TSE) and Fast Spin-Echo (FSE) sequences are multi-echo spin-echo implementations based on the CPMG conditions. To reduce power deposition, the prescribed flip angle for TSE or FSE refocusing pulses may be less than 180 degrees. TSE/FSE sequences will usually apply different phase-encoding for each refocusing pulse, to accelerate the scan by acquiring multiple k-space lines per excitation pulse.

Alternative T2 models

Alternative T2-mapping sequences do not produce the traditional T2 decay curve but are still able to fit T2 maps using other signal models. For example, Magnetic Resonance Fingerprinting (MRF) [Ma2013] uses pseudo-random acquisition parameters to induce seemingly random signal timecourses with many fluctuations. MRF is based on the principle that each T2 species will produce a unique signal “curve” if the acquisition parameters are appropriate.

Clinical applications

Examples of T2 mapping for clinical applications are heart muscle, articular cartilage, and epilepsy. For temporal lobe epilepsy, T2 mapping has a role to play in assessing T2 changes in the Hippocampus caused by sclerosis, alongside Hippocampal volume measurements. Hippocampal sclerosis is associated with increased T2, indicating there is a clinical need for reliable measurement of T2 [Winston2017].

References and Further Reading:

  • Allen J. An Optimisation Framework for Magnetic Resonance Fingerprinting. Thesis. 2019.
  • Meiboom S, Gill D. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Review of Scientific Instruments. 1958;29(8):688-691. doi:10.1063/1.1716296
  • Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192. doi:10.1038/nature11971
  • Hennig J, Nauerth A, Friedburg H. RARE imaging – a fast imaging method for clinical MR. Magn Reson Med 1986; 3: 823-833. 
  • Fast Spin Echo (“Turbo Spin Echo”) https://mriquestions.com/what-is-fsetse.html
  • Spin Echo Variations https://mriquestions.com/se-vs-multi-se-vs-fse.html
  • CPMG conditions for FSE\TSE. https://www.mr-tip.com/serv1.php?type=db1&dbs=CPMG
  • Paul Callaghan Talk on Spin Echoes, CPMG and T2 relaxation. https://www.azom.com/materials-video-details.aspx?VidID=1678
  • Rad229 (2020) Lecture-08B: Practical Spin-Echo-Train Signals.; 2020. https://www.youtube.com/watch?v=rp3rwuZlPyU. Accessed September 6, 2023.
  • Winston GP, Vos SB, Burdett JL, Cardoso MJ, Ourselin S, Duncan JS. Automated T2 relaxometry of the hippocampus for temporal lobe epilepsy. Epilepsia. 2017;58(9):1645-1652. doi:10.1111/epi.13843
  • Deoni SCL, Rutt BK, Peters TM. Rapid combinedT1 andT2 mapping using gradient recalled acquisition in the steady state. Magn Reson Med. 2003;49(3):515-526. doi:10.1002/mrm.10407
  • Deoni SCL, Peters TM, Rutt BK. High-resolutionT1 andT2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn Reson Med. 2005;53(1):237-241. doi:10.1002/mrm.20314
  • Homer J, Beevers MS. Driven-equilibrium single-pulse observation of T1 relaxation. A reevaluation of a rapid “new” method for determining NMR spin-lattice relaxation times. Journal of Magnetic Resonance (1969). 1985;63(2):287-297. doi:10.1016/0022-2364(85)90318-X
  • Milford D, Rosbach N, Bendszus M, Heiland S. Mono-Exponential Fitting in T2-Relaxometry: Relevance of Offset and First Echo. Fan X, ed. PLoS ONE. 2015;10(12):e0145255. doi:10.1371/journal.pone.0145255
  • Gudbjartsson H, Patz S. The rician distribution of noisy mri data. Magnetic Resonance in Medicine. 1995;34(6):910-914. doi:10.1002/mrm.1910340618
  • He T, Gatehouse PD, Smith GC, Mohiaddin RH, Pennell DJ, Firmin DN. Myocardial T2* Measurements in Iron Overloaded Thalassemia. Magn Reson Med. 2008;60(5):1082-1089. doi:10.1002/mrm.21744
  • Miller AJ, Joseph PM. The use of power images to perform quantitative analysis on low SNR MR images. Magn Reson Imaging. 1993;11(7):1051-1056. doi:10.1016/0730-725x(93)90225-3
Tutorials